DFS-Recall9

发表于 分类于 ，

题目描述[原题链接][https://leetcode-cn.com/problems/sudoku-solver/]

编写一个程序，通过已填充的空格来解决数独问题。

一个数独的解法需遵循如下规则：

数字 1-9 在每一行只能出现一次。
数字 1-9 在每一列只能出现一次。
数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。
空白格用 '.' 表示。
img
一个数独。
img

答案被标成红色。

Note:

给定的数独序列只包含数字 1-9 和字符 '.' 。
你可以假设给定的数独只有唯一解。
给定数独永远是 9 x 9 形式的。

算法描述

使用的概念

了解两个编程概念会对接下来的分析有帮助。

第一个叫做 约束编程。

基本的意思是在放置每个数字时都设置约束。在数独上放置一个数字后立即
排除当前 行， 列 和 子方块 对该数字的使用。这会传播 约束条件 并有利于减少需要考虑组合的个数。

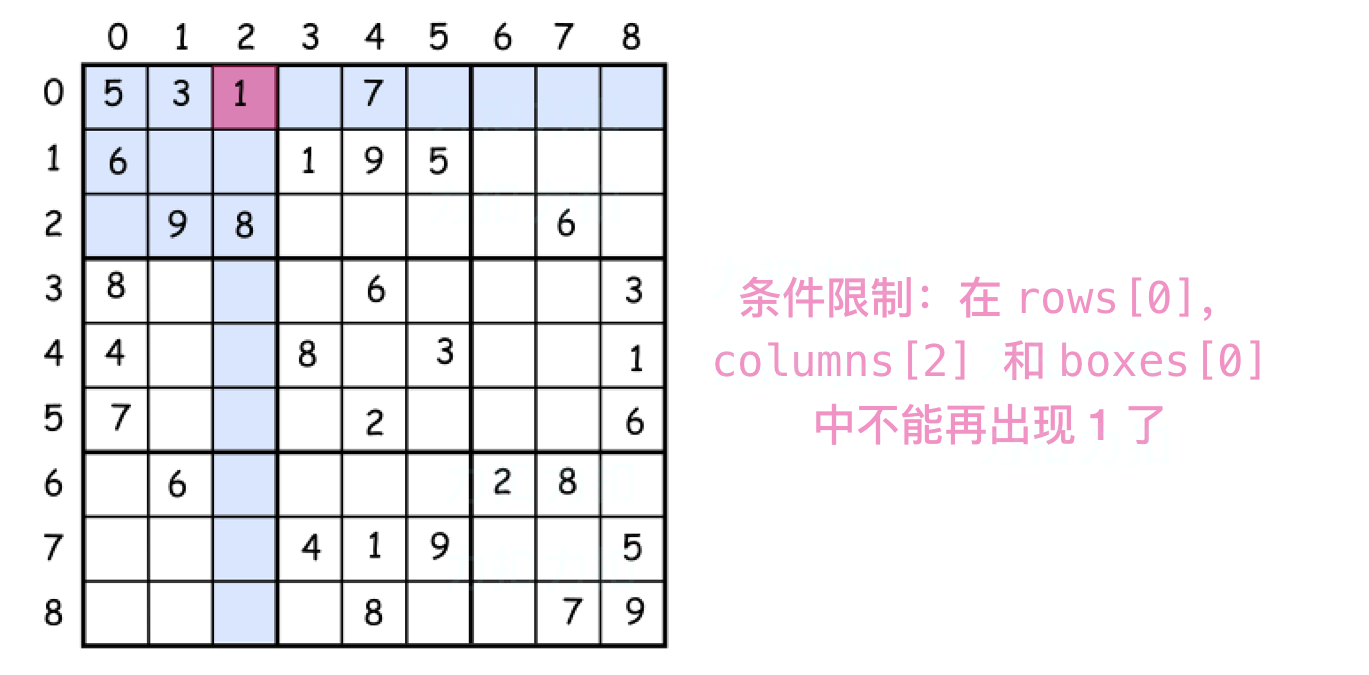
37_const3.png

第二个叫做 回溯。

让我们想象一下已经成功放置了几个数字
在数独上。
但是该组合不是最优的并且不能继续放置数字了。该怎么办？ 回溯。
意思是回退，来改变之前放置的数字并且继续尝试。如果还是不行，再次 回溯。

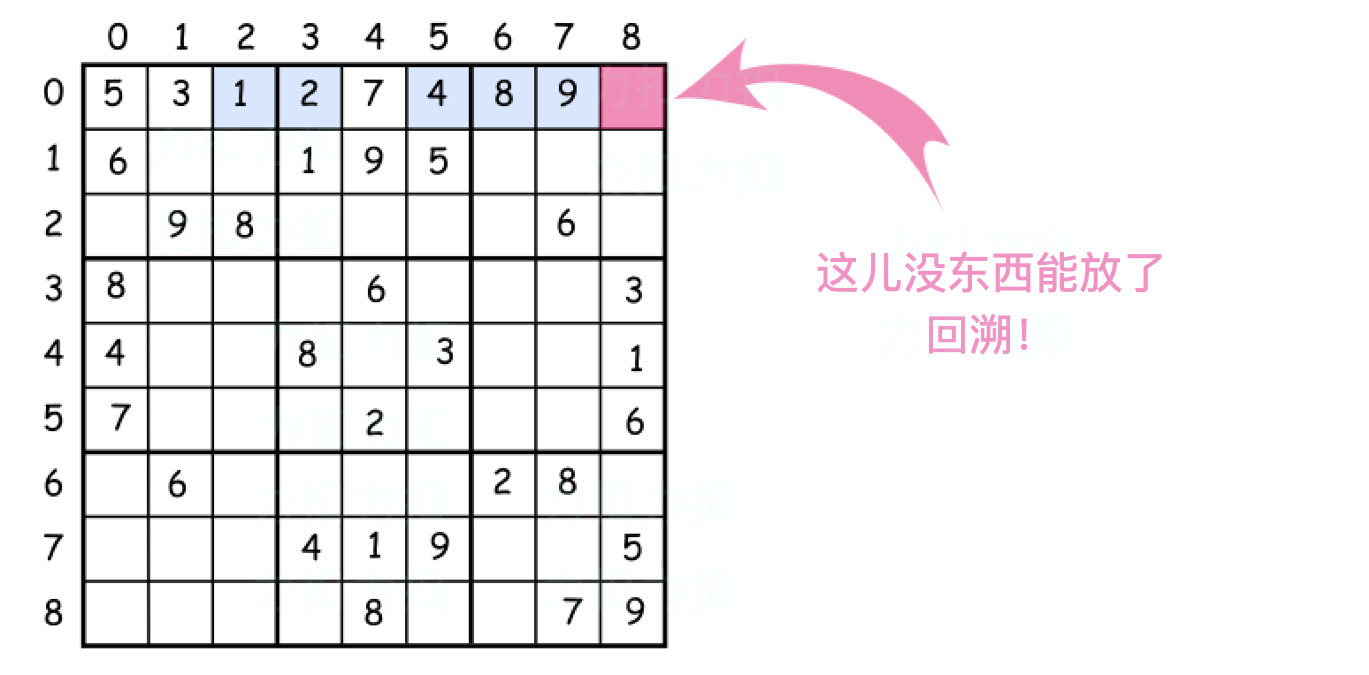
37_backtrack2.png

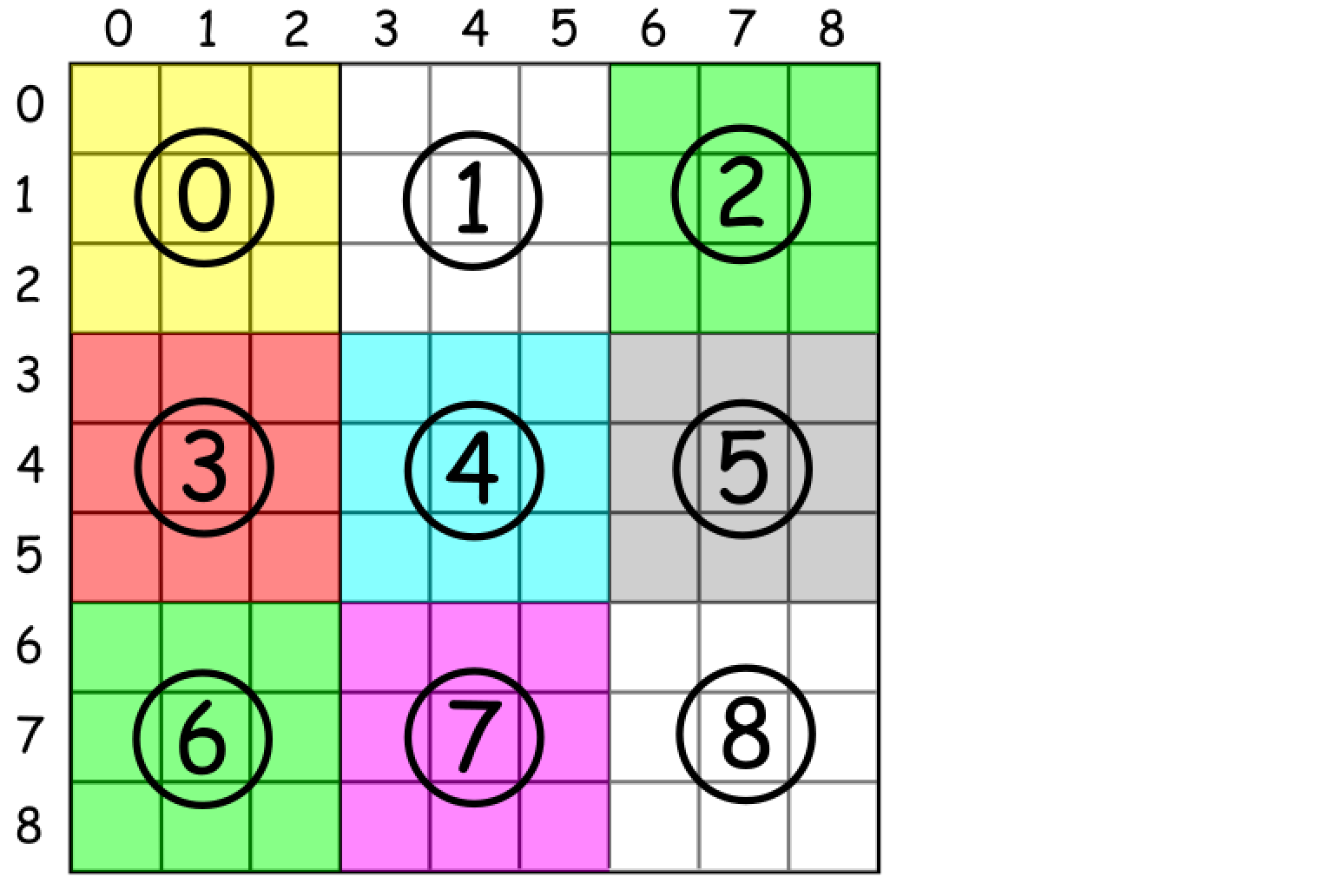
如何枚举子方块

一种枚举子方块的提示是：

使用 方块索引= (行 / 3) * 3 + 列 / 3
其中 / 表示整数除法。

36_boxes_2.png

算法

现在准备好写回溯函数了
backtrack(row = 0, col = 0)。

  • 从最左上角的方格开始 row = 0, col = 0。直到到达一个空方格。

  • 从1 到 9 迭代循环数组，尝试放置数字 d 进入 (row, col) 的格子。

    • 如果数字 d 还没有出现在当前行，列和子方块中：

      • 将 d 放入 (row, col) 格子中。

      • 记录下 d 已经出现在当前行，列和子方块中。

      • 如果这是最后一个格子

        row == 8, col == 8：

        • 意味着已经找出了数独的解。

      • 否则

        • 放置接下来的数字。

      • 如果数独的解还没找到：

      • 将最后的数从 (row, col) 移除。

C++代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
class Solution {
public:

     bool solved = 0;
	bool row[9][10], col[9][10], box[9][10];
	void solveSudoku(vector<vector<char>>& board) {
		memset(row, 0, sizeof(row));
		memset(col, 0, sizeof(col));
		memset(box, 0, sizeof(box));
		for(int i=0;i<9;i++)
			for (int j = 0; j < 9; j++) {
				if (board[i][j] == '.') continue;
				int index = i / 3 * 3 + j / 3;
				int num = board[i][j] - '0';
				row[i][num] = col[j][num] = box[index][num] = 1;
			}
		DFS(0, 0, board);
	}
	void DFS(int i, int j, vector<vector<char>>& board) {
		if (i == 9) { solved = 1; return; }	
		if (board[i][j] != '.') {				
			if (j < 8) DFS(i, j + 1, board);
			else DFS(i + 1, 0, board);
		}
		else {			
			int index = i / 3 * 3 + j/3;
			for (int num = 1; num <= 9; num++) {
				if (!row[i][num] && !col[j][num] && !box[index][num]) {
					board[i][j] = num + '0';
					row[i][num] = col[j][num] = box[index][num] = 1;
					if (j < 8) DFS(i, j + 1, board);
					else DFS(i + 1, 0, board);
					if (!solved) { //回溯
						row[i][num] = col[j][num] = box[index][num] = 0;
						board[i][j] = '.';
					}
				}
			}
		}
	}
};

Java代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
class Solution {
  // box size
  int n = 3;
  // row size
  int N = n * n;

  int [][] rows = new int[N][N + 1];
  int [][] columns = new int[N][N + 1];
  int [][] boxes = new int[N][N + 1];

  char[][] board;

  boolean sudokuSolved = false;

  public boolean couldPlace(int d, int row, int col) {
    /*
    Check if one could place a number d in (row, col) cell
    */
    int idx = (row / n ) * n + col / n;
    return rows[row][d] + columns[col][d] + boxes[idx][d] == 0;
  }

  public void placeNumber(int d, int row, int col) {
    /*
    Place a number d in (row, col) cell
    */
    int idx = (row / n ) * n + col / n;

    rows[row][d]++;
    columns[col][d]++;
    boxes[idx][d]++;
    board[row][col] = (char)(d + '0');
  }

  public void removeNumber(int d, int row, int col) {
    /*
    Remove a number which didn't lead to a solution
    */
    int idx = (row / n ) * n + col / n;
    rows[row][d]--;
    columns[col][d]--;
    boxes[idx][d]--;
    board[row][col] = '.';
  }

  public void placeNextNumbers(int row, int col) {
    /*
    Call backtrack function in recursion
    to continue to place numbers
    till the moment we have a solution
    */
    // if we're in the last cell
    // that means we have the solution
    if ((col == N - 1) && (row == N - 1)) {
      sudokuSolved = true;
    }
    // if not yet
    else {
      // if we're in the end of the row
      // go to the next row
      if (col == N - 1) backtrack(row + 1, 0);
        // go to the next column
      else backtrack(row, col + 1);
    }
  }

  public void backtrack(int row, int col) {
    /*
    Backtracking
    */
    // if the cell is empty
    if (board[row][col] == '.') {
      // iterate over all numbers from 1 to 9
      for (int d = 1; d < 10; d++) {
        if (couldPlace(d, row, col)) {
          placeNumber(d, row, col);
          placeNextNumbers(row, col);
          // if sudoku is solved, there is no need to backtrack
          // since the single unique solution is promised
          if (!sudokuSolved) removeNumber(d, row, col);
        }
      }
    }
    else placeNextNumbers(row, col);
  }

  public void solveSudoku(char[][] board) {
    this.board = board;

    // init rows, columns and boxes
    for (int i = 0; i < N; i++) {
      for (int j = 0; j < N; j++) {
        char num = board[i][j];
        if (num != '.') {
          int d = Character.getNumericValue(num);
          placeNumber(d, i, j);
        }
      }
    }
    backtrack(0, 0);
  }
}