advancing8

发表于 分类于 ，

题目描述[原题链接][https://leetcode-cn.com/problems/largest-rectangle-in-histogram/]

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

img

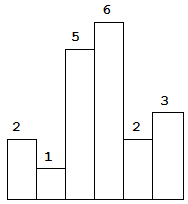
以上是柱状图的示例，其中每个柱子的宽度为 1，给定的高度为 [2,1,5,6,2,3]。

img

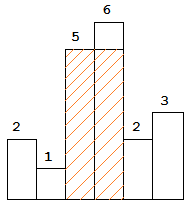
图中阴影部分为所能勾勒出的最大矩形面积，其面积为 10 个单位。

示例:

1
2
输入: [2,1,5,6,2,3]
输出: 10

算法描述

首先向栈中插入一个-1作为最小的下标，然后遍历数组，如果插入值比栈顶值大继续插入编号，如果heights[sta.top()]>=heights[i]则要更新最大长度,即mx = max(mx,height[i]*(sta.top()-i-1))更新最大值，将数组数据压入结束后，再用相同的公式把栈弹空即可，返回最后的最大值；

C++代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        int len = heights.size();
        heights.push_back(0);
        stack<int> s;
        int area = 0;
        for(int i=0;i<len+1;i++)
        {
            while(!s.empty()&&heights[s.top()]>heights[i])
            {
                int h = heights[s.top()];
                s.pop();
                area = max(area,h*(s.empty()?i:(i-s.top()-1)));
            }
            s.push(i);
        }
        return area;
    }
};

Java代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
    public int largestRectangleArea(int[] heights) {
        Stack<Integer> sta = new Stack<Integer>();
        sta.push(-1);
        int max = 0;
        for(int i = 0;i<heights.length;i++){
            while(sta.peek()!=-1&&heights[sta.peek()]>=heights[i]){
                max = Math.max(max,heights[sta.pop()]*(i-sta.peek()-1));
            }
            sta.push(i);
        }
        while(sta.peek()!=-1)
            max = Math.max(max,heights[sta.pop()]*(heights.length - sta.peek()-1));
        return max;
    }
}